Calculating Triangle Normals

Unity’s Mesh class nicely exposes the mesh’s topology and allows us to manipulate it with ease. The access to vertex positions, triangles and normals is immediate thanks to the availability of properties like Mesh.vertices, Mesh.triangles and Mesh.normals.

Nonetheless, all developers who do any wizardry on meshes unavoidably come across a blind spot: triangle normals.

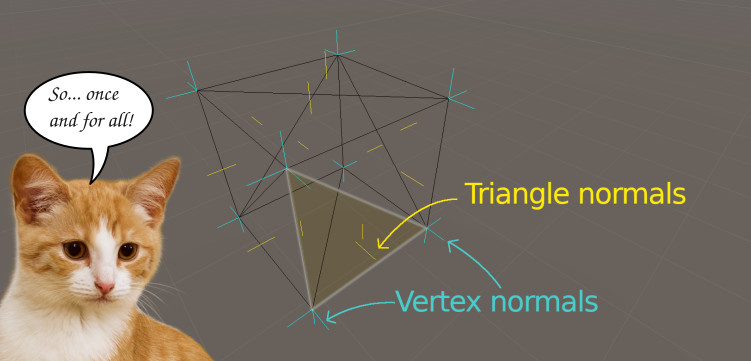
Many think that Mesh.normals will give enough intormation to know what way the triangle is facing but they soon discover that the vectors that come with Mesh.normals are vertex normals and are very different from triangle normals.

When do we need triangle normals?

Vertex normals hold information about the topology at the point specified by the vertex; unfortunately they don’t hold any interesting information about the direction the triangle is pointing towards. At least not directly. In fact, when you need to know exactly the vector that is normal to the plane defined by a triangle, you need to compute it yourself.

The number of cases where face normals or triangle normals must be known are endless. To name a few:

How to compute triangle normals

Calculating the triangle normals involves some basic vector algebra. We will use Vector3.Cross and Vector3.Dot.

The idea is to convert two of the triangle’s sides into vectors and compute their cross product, which will give us one of the two possible normals to the triangle. We then use one of the normals at the vertices (part of mesh data) as a spy to see if we are on the right side. Comparing the result of the cross product and our spy vertex normal by using a dot product tells us if we must invert the cross product result.

Finally we can store the found triangle normal.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


private Vector3[] ComputeMeshTriangleNormals(Mesh mesh)
{
    int trisCount = mesh.triangles.Length / 3;
    Vector3[] normals = new Vector3[trisCount];
    int[] triangles = mesh.triangles;
    for (int i = 0; i < trisCount; i++)
    {
        int indexA = triangles[i * 3];
        int indexB = triangles[i * 3 + 1];
        int indexC = triangles[i * 3 + 2];
        Vector3 A = mesh.vertices[indexA];
        Vector3 B = mesh.vertices[indexB];
        Vector3 C = mesh.vertices[indexC];
        // find one of the two possible normals
        Vector3 normal = Vector3.Cross(B - A, C - A).normalized;
        // now use the vertex normal to check if the found normal needs inverting
        if(Vector3.Dot(normal, mesh.normals[indexA]) < 0f)
        {
            normal = -normal;
        }
        normals[i] = normal;
    }
    return normals;
}

Gizmo test

Here we want to quickly show the result of our calculation. For this we use Unity’s OnDrawGizmosSelected method which is handy to draw some visual clues in the Scene View.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


private void OnDrawGizmosSelected()
{
    if(mesh == null)
    {
        return;
    }

    Gizmos.matrix = transform.localToWorldMatrix;

    Gizmos.color = Color.black;
    Gizmos.DrawWireMesh(mesh);

	// Draw vertex normals that are commonly available via Mesh.normals
    Gizmos.color = Color.cyan;
    for (int i = 0; i < mesh.vertices.Length; i++)
    {
        Vector3 normal = mesh.normals[i];
        Gizmos.DrawLine(mesh.vertices[i], mesh.vertices[i] + normal * gizmosNormalLength);
    }

    Gizmos.color = Color.yellow;
    Vector3[] normals = ComputeMeshTriangleNormals(mesh);

    for (int i = 0; i < mesh.triangles.Length / 3; i++)
    {
        int indexA = mesh.triangles[i*3];
        int indexB = mesh.triangles[i*3 + 1];
        int indexC = mesh.triangles[i*3 + 2];
        Vector3 avgVertex = 0.333f * (mesh.vertices[indexA] + mesh.vertices[indexB] + mesh.vertices[indexC]);
        Gizmos.DrawLine(avgVertex, avgVertex + normals[i] * gizmosNormalLength);
    }
}

Another snap showing the results on a capsule.

Wrong Method: average of vertex normals

Do not fall into the trap of calculating the triangle normals by averaging the normals at the vertices. Such method will give you the real normal to the triangle’s plane in very few isolated cases but will normally fail, especially at mesh borders.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


private Vector3[] ComputeWrongMeshTriangleNormals(Mesh mesh)
{
    int trisCount = mesh.triangles.Length / 3;
    Vector3[] normals = new Vector3[trisCount];
    int[] triangles = mesh.triangles;
    for (int i = 0; i < trisCount; i++)
    {
        int indexA = triangles[i * 3];
        int indexB = triangles[i * 3 + 1];
        int indexC = triangles[i * 3 + 2];
        Vector3 normalA = mesh.normals[indexA];
        Vector3 normalB = mesh.normals[indexB];
        Vector3 normalC = mesh.normals[indexC];
        Vector3 avgNormal = 0.3333f * (normalA + normalB + normalC);
        normals[i] = avgNormal;
    }
    return normals;
}

Share this page: